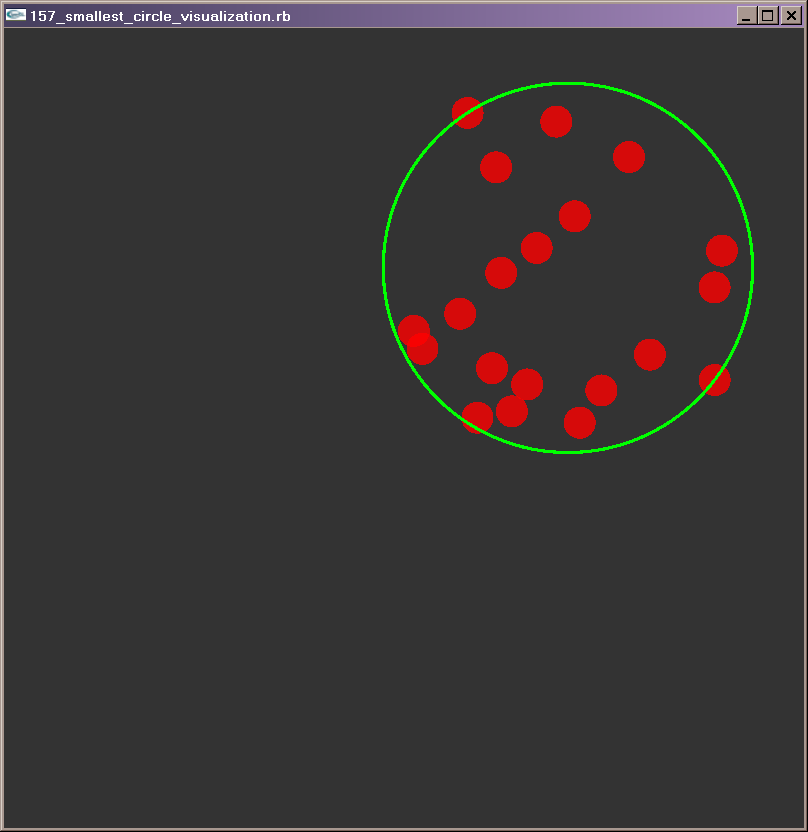
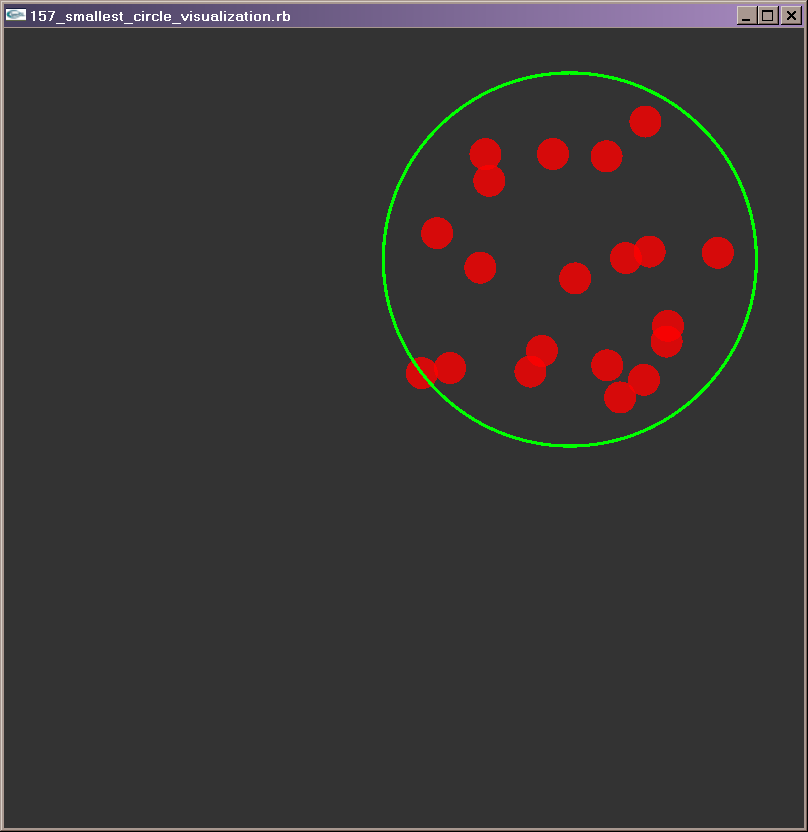
First, I want to thank everyone participating and watching this week
for being patient with me while I was down with the flu. I am almost
completely recovered at this point, and I hope that doesn't come back
for a good, long time.
Second, thanks to all quizzers who made an attempt at the quiz, even
after the scary warning I made about the difficulty.
Third, I had hoped to provide a set of tests to help quizzers check
their solutions, but the flu hit me pretty hard and I was unable. A
special thanks go to Bill Kelly, Thomas ML and Lionel Bouton; they
took time to benchmark the solutions for both speed and accuracy, when
I didn't have the ability to do it.
Now, about the smallest enclosing circle problem... I warned from the
start that the problem might prove more difficult than it appears.
It's a problem that has been attacked and solved numerous times. [1][2]
[3][4][5]
One easy to understand algorithm was originally described by Welzl[6],
and Rick DeNatale *almost* came up with the same answer:
The basic approach is to start with a circle containing only the first point,
and then add the points one by one changing the circle as necessary. So:
First point
Set center to the point and radius to zero.
Subsequent points.
If the point is already in the circle then the point is simply added to
the collection of points and the circle is unchanged....
If the point is further from the center than the radius, the we know that
it must lie on the circumference of the new circle which will contain all
of the points examined thus far.
The point where Rick's propsed algorithm fails is in determining what
other points will be part of the circle's boundary.
I don't intend to get into the finer details of these algorithms here;
I've provided a number of references for those who are interested in
crafting an exact solution. In particular, Douglas Seifert did provide
such a solution.
The solution I am going to examine here is that of Frank Fischer,
whose solution is actually the slowest according to the benchmarks.
However, his solution was consistently close, simple to understand,
and provides a technique that can be used for many kinds of problems,
perhaps not always for speed but sometimes for sanity.
Frank's Circle class is identical to that provided by the quiz, so
I'll skip that. Let's look at his modified Point class:
class Point
def initialize( *coords )
@coords = coords.map{|x| x.to_f}
end
The initializer takes an array of numbers, rather than just the two
that my original Point class (derived from Struct) provided. Frank's
goal is to support more than just two dimensions; in fact, his
solution will work with any dimensions. The asterisk placed in front
of the parameter name means that the caller doesn't need to
specifically provide an array... just the content. So the call:
p = Point.new(1, 2, 3, 4, 5)
Will set coords to the array [1, 2, 3, 4, 5] inside the initializer.
The initializer stores these numbers away after ensuring they all look
like floats.
def size
@coords.size
end
def ( index )
@coords[index]
end
def = ( index, x )
@coords[index] = x
end
def self.random( n = 2 )
Point.new( *(1..n).map{ 0.5 - rand } )
end
def +(p)
return Point.new( *(0...size).map{|i| @coords[i] +
p[i]} )
end
def -(p)
return Point.new( *(0...size).map{|i| @coords[i] -
p[i]} )
end
def *(a)
return Point.new( *@coords.map{|x| x * a} )
end
def /(a)
return Point.new( *@coords.map{|x| x / a} )
end
# calculate the inner product if this point with p
def ip(p)
(0...size).inject(0) { |sum, i| sum + @coords[i] * p[i] }
end
def to_s
"(#{@coords.join(', ')})"
end
end
Frank adds a number of arithmetic support functions for his Point
class. Looking at this reminds me of the standard library class
Vector... and it's not surprising, as the intent of the Point class
overlaps significantly with the Vector class. I hoped someone might
make use of Vector; alas, I think the starting code I provided was
probably a bit too suggestive. Lesson learned.
Next we break down Frank's evaluation function.
def evaluate( m, points )
y_big = nil
grad = nil
Here, m is a point to evaluate as the center of a circle, and points
is the list of points that need to be enclosed. This function aims to
calculate two things. First, y_big is the minimum radius of a circle
centered at m that would enclose all the points. (Actually, it's the
square of the radius, which is a simpler calculation that avoids the
costly Math.sqrt function.) Second, grad is the gradient, which I'll
explain later.
y_big and grad both start out invalid, but provided we have at least
one point to enclose, they will both have values at the end. Now we
loop over all the points.
points.each do |p|
d = (m - p)
Here, d is the delta between the circle's center and the current
point. It's a vector, which means it has direction (pointing at m from
p) and length (the distance from p to m).
y = d.ip( d )
Function ip is documented by Frank as the inner product (also known as
the dot product). The inner product has a number of uses. In this
particular case, taking the inner product of d against itself gives us
the squared length of d. If we come back to the idea that we're trying
to find a circle, if m is the center and p is on the circle, then the
length of d would be the radius. So y is the radius squared.
if y_big.nil? or y > y_big
y_big = y
grad = d*2
end
end
Now we check to see if y is the largest squared radius we've found so
far; if so, remember it. Otherwise, keep the existing largest squared
radius y_big. Hit the end of the loop and keep checking points.
In order to enclose all the points, we remember the largest squared
radius y_big. One way to shrink that radius in a future iteration is
to move the center towards the point farthest away from our current
center m. Above, we mentioned that d was a vector that pointed away
from p towards m. That's exactly the direction we're looking for...
well, exactly the opposite direction, but that's easily remedied by
using subtraction later rather than addition. So d is scaled (by two,
maintaining direction but with length equal to the diameter) and
assigned to grad.
return [y_big, grad]
end
Once all points have been examined, we return the largest squared
radius and the corresponding gradient. Now let's look at Frank's final
function that makes use of this evaluation.
def encircle( points,
x_start = Point.new( *([0]*points[0].size) ),
max_iter = 100 )
Frank's encircle function takes extra arguments, but provides sensible
defaults so that it still matches the quiz's requirements. x_start is
a point at the origin (i.e. all components are zero) which Frank uses
as the initial guess for the circle's center. max_iter is the number
of iterations performed in an attempt to narrow down the best answer.
x = x_start
y, g = nil, nil
for k in 1..max_iter do
y, g = evaluate( x, points ) # step 1
x = x - g/k # step 2
end
We run in a loop max_iter times, repeating two simple steps.
First, we evaluate the "fitness" of the current circle center x given
the list of points that we need to enclose. This function we described
above, and gives us back y as the squared radius of the circle and g
as the gradient used for improving upon our initial guess.
Second, we compute a new circle center x by moving it along the
gradient. As mentioned earlier, the gradient points toward the
circle's center and away from the furthest point; by subtracting it
here, that moves the new circle's center towards the furthest point in
the hope that will reduce the largest radius.
If we kept moving the circle's center about by the full length of the
gradient, we'd keep jumping around without ever narrowing in on a
solution. The answer to this problem is to scale down the gradient by
k which increases each iteration. So initial jumps are large, but each
additional jump is less and less.
return Circle.new(x, Math.sqrt(y))
end
After all iterations are done, we now have a circle. Since y has
always been the square of the radius, we finally take its square root
to get the true radius.
Note that this is not an exact solution to the quiz problem, but it
has shown to consistently come reasonably close to the exact solution.
And sometimes reasonably close is sufficient. The reason I picked
Frank's solution is not for its exactness nor its speed, but because
it is an elegant demonstration of a general technique. If you can
provide a fitness function (in our case, the circle radius) and some
sort of gradient, you can consider this technique for other problems.
Thanks to everyone who participated in this first quiz of mine.
Tomorrow we'll have something very simple that'll get everyone saying,
"Hello!".
[1] Smallest Enclosing Circle Problem
[2] Min_sphere_of_spheres_d<Traits>
[3] http://www.inf.ethz.ch/personal/gaertner/miniball.html
[4] http://www.cs.mcgill.ca/~cs507/projects/1998/jacob/problem.html
[5]
http://citeseer.ist.psu.edu/cache/papers/cs/30066/http:zSzzSzpage.inf.fu-berlin.dezSz~svenzSzown_workzSzmin-circle_impl_tr-b-98-04.pdf/smallest-enclosing-circles-an.pdf
[6] http://citeseer.ist.psu.edu/235065.html